逆合成孔径雷成像（一）— 傅里叶变换基础1
本文共 651 字，大约阅读时间需要 2 分钟。
逆合成孔径雷达成像（一）— 傅里叶变换基础1
傅里叶变换是一种非常常见并且实用的数学工具，特别是在分析随机信号，解决先行问题。傅里叶变换可以简单的定义为一个线性算子，目的是将一个域中的函数或者信号映射到另外一个域中以其他形式函数或者信号表示。
在信号与系统中，傅里叶变换常用的方法是将信号从时域变换到频域，或者从频域变换到时域。目的就是为了好算。
1.傅里叶变换公式
傅里叶正变换：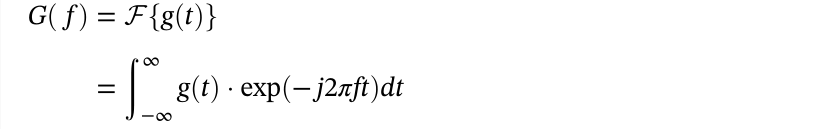
更通俗地来讲，傅里叶变化是把一个信号分解为无穷多个正弦信号或者复指数信号的叠加。 傅里叶反变换:
2.傅里叶变换的常用性质 2.1 线性（同时满足齐次性和叠加性） 
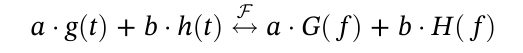2.2 时域平移 
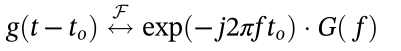2.3 频域平移 
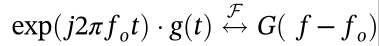2.4 伸缩变换 
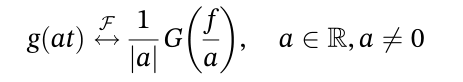2.5 时域反转 
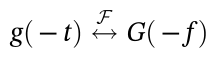2.6 时域共轭 
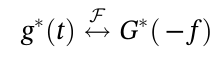2.7 时域相乘 
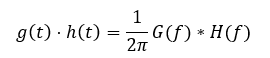2.8 时域卷积
2.9 时域微分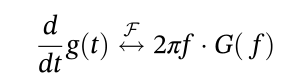 
2.10 时域积分 
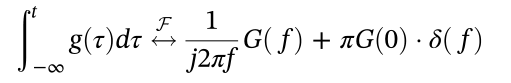2.11 帕斯瓦尔定理 
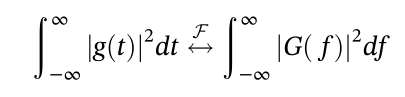傅里叶变换的概念能够很好地用于平稳信号，但是在真实世界中的信号，其频率内容随时间而变化。为了能够显示这些频率随时间的变化；因此，可以使用joint time–frequency（JTF)来表示。 下一节将详细描述JTF。欢迎关注。
[1] Caner Ozdemir - Inverse Synthetic Aperture Radar Imaging With MATLAB Algorithms-John Wiley & Sons (2021)
转载地址：http://awfr.baihongyu.com/
你可能感兴趣的文章
SVN Unable to connect to a repository at URL 的解决方案
查看>>
OSI 7 层网络模型
查看>>
JDK 内置的多线程协作工具类的使用场景
查看>>
Java 中哪些对象可以获取类对象
查看>>
linux 的 sleep 命令
查看>>
11.2.6 时间值的小数秒
查看>>
Redis源码分析（七）--- zipmap压缩图
查看>>
自定义Hive Sql Job分析工具
查看>>
【MySQL】（九）触发器
查看>>
关于Altium Designer 09导出BOM表不能正确分类问题
查看>>
Oracle 11G环境配置
查看>>
【Python】（十二）IO 文件处理
查看>>
【Oozie】（三）Oozie 使用实战教学，带你快速上手！
查看>>
师兄面试遇到这条 SQL 数据分析题，差点含泪而归！
查看>>
C语言的数值溢出问题(上)
查看>>
BottomNavigationView控件item多于3个时文字不显示
查看>>
函数指针的典型应用-计算函数的定积分(矩形法思想)
查看>>
8051单片机(STC89C52)以定时器中断模式实现两倒计时器异步计时
查看>>
用 wxPython 打印你的 App
查看>>
vue项目通过vue.config.js配置文件进行proxy反向代理跨域
查看>>